
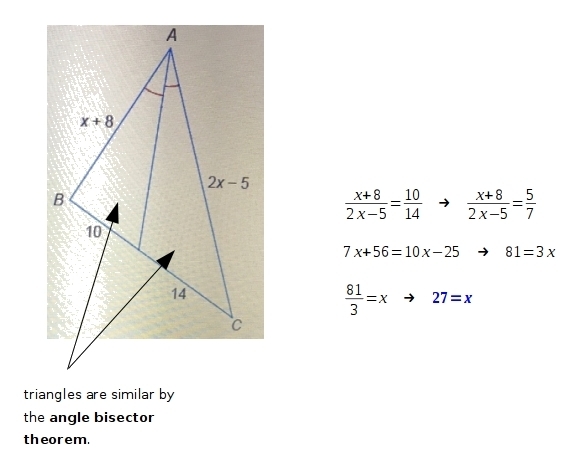
Solution: Let's start by drawing a diagram (which is not necessarily to scale). Practice Problem: Two isosceles triangles both have an interior angle of 100°. As a result, by the angle-angle condition, all equilateral triangles must be similar to one another. Solution: We know from our study of triangles that an equilateral triangle contains three congruent angles thus, the measure of each angle in an equilateral triangle is 60°.
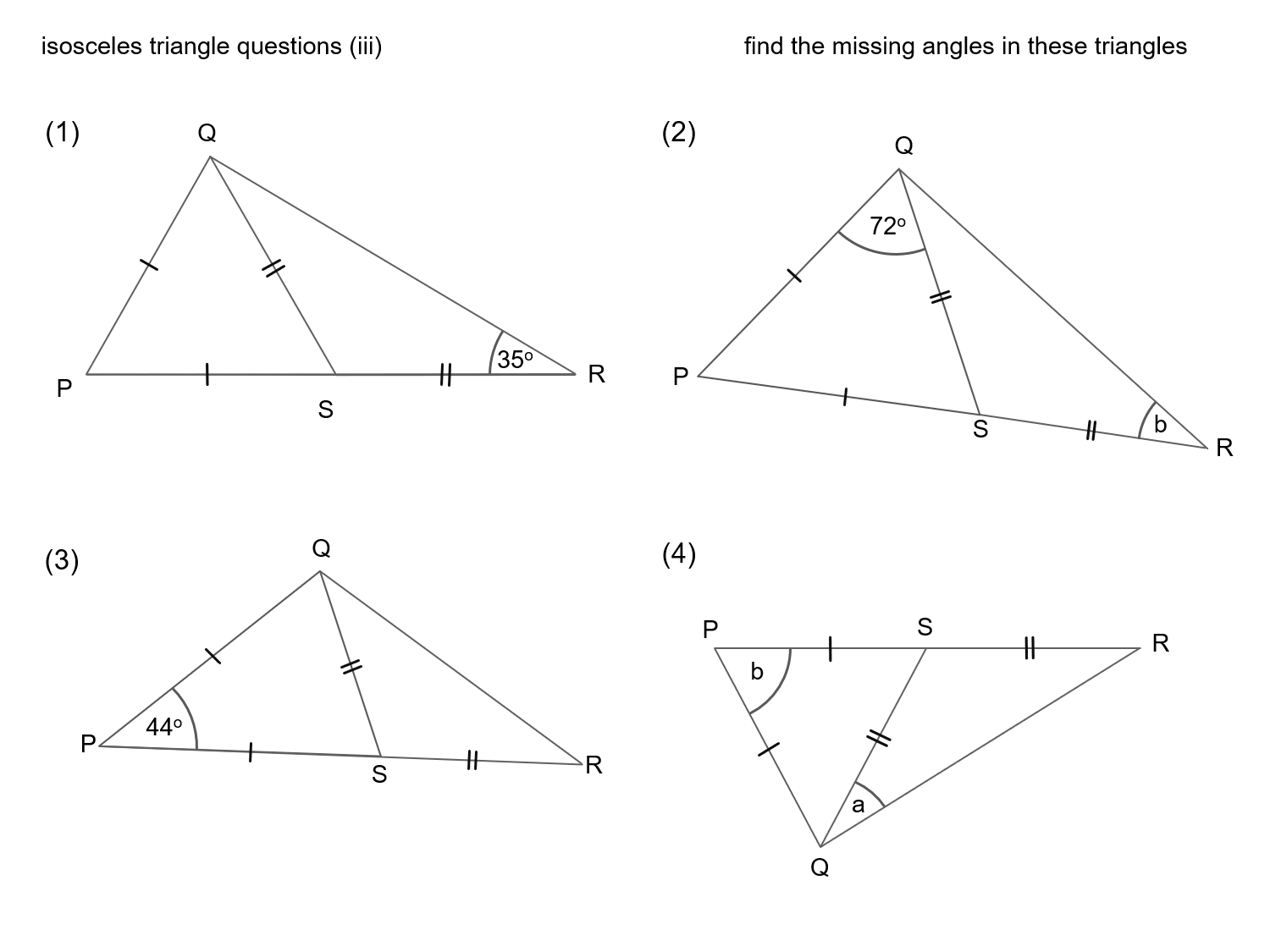
Practice Problem: Prove that any two equilateral triangles are similar. Thus, we have shown the two triangles to be similar.
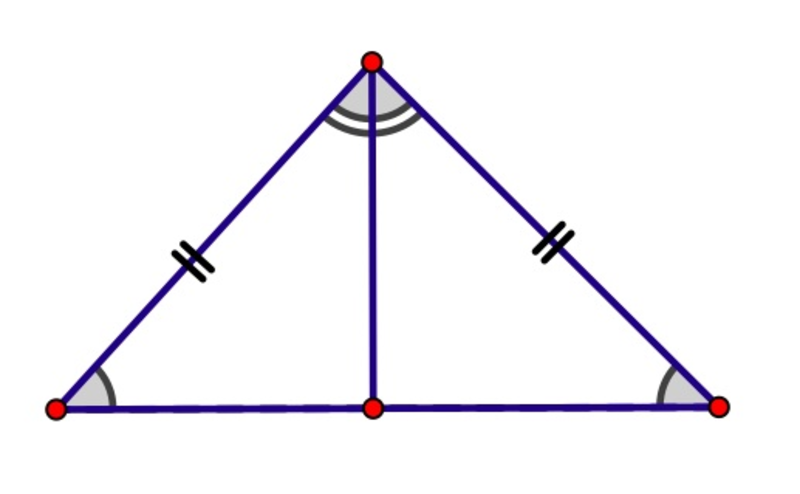
Triangles ABD and BCD Side-angle-side (proportionality) condition Sides BC and BD, and Statements 2 and 3ĥ. We can also separate the triangles for clarity.Ĥ. Note that the triangles have congruent angles and. Solution: Let's prove that the triangles are similar using a two-column proof format. Practice Problem: Prove that triangles ABD and BCD are similar. Thus, using any of the above criteria, we can prove that two triangles are congruent. These two triangles are similar because the corresponding labeled sides are proportional (the length of the sides for the rightmost triangle are 5/3 times the lengths of the sides for the leftmost triangle) and the corresponding included angles are congruent.


 0 kommentar(er)
0 kommentar(er)
